Table of Contents
Response Surface Methodology
To build an empirical model, the statistical and mathematical collection is called the Response Surface Methodology (RSM). The main objective of RSM is to maximize production by optimizing the response (output variable), which is influenced by several independent variables (input variables). Response surface methodology is proved to be useful for improving, developing, and optimizing processes. It is an advanced tool having three factorial designs involving several input variables and their corresponding relationship with one or more measured dependent responses. To date, the RSM has been broadly used in several fields such as:
- Food processing and beverages
- Chemical process
- Analytical chemistry
- Biochemical processes
- Industrial
Origin of Response Surface Methodology
In 1951, it was introduced by George EP Box and Wilson KB with a basic idea of the sequence of experiments to get an optimal response.
Main Purpose of Response Surface Methodology
RSM is a tool of a statistical approach to optimize a process, generally employed to maximize the production of a targeted substance by optimization of independent variables. It is widely used for multiple regression analysis using quantitative data, that would get suitably designed experiments to explain multivariate equations concurrently. Extensive use of RSM becomes just because of conventional methods, in the conventional methods interaction among process variables is determined by statistical techniques. An experiment is a series of tests, called runs, in which changes are made in the input variables (independent) to identify the reasons for changes in the output (dependent) response. It provides the interactive effects of process input variables and their consequent effects on response is graphical represented and discussed. The aim is to search for the optimum spot where the response (output) is either minimized or maximized (depends on the target). The models that will use as:
For example: If we take two input parameters as X1 and X2, one response as Y. See the below figure….

Modeling
It can be carried out by using the following steps
- Identification of the important independent variables with their upper and lower limits.
- Development of the design matrix.
- Perform experiments as per runs generated by software (see design matrix).
- Put the values of response parameters in the design matrix
- Check the model fitting either (linear, 2 FI, or quadratic)
- Develop a suggested model and calculate the regression coefficients.
- Check the adequacy of the suggested model.
- Test the significance of coefficients.
- Analyze the results
- Numerical optimization
To understand the complete procedure in Response Surface Methodology, see the following flow chart:

Types of Response Surface Methodology Design
There are two main types of response surface designs:
Central Composite designs (CCD)
It is a factorial or fractional factorial design with center points, augmented with a group of axial points (also called star points) that will estimate the curvature. It is generally used to:
- Efficiently estimate first- and second-order terms.
- Model a response variable with curvature by adding center and axial points to a previously done factorial design.
- When the design plan calls for sequential experimentation
- Can be done in stages such as factorial + center points + axial points
- In this design, each factor varies over five levels
- Extreme high (star point)
- High
- Center
- Low
- Extreme low (star point)
See the below figure to understand the origination of Central Composite Design (CCD)
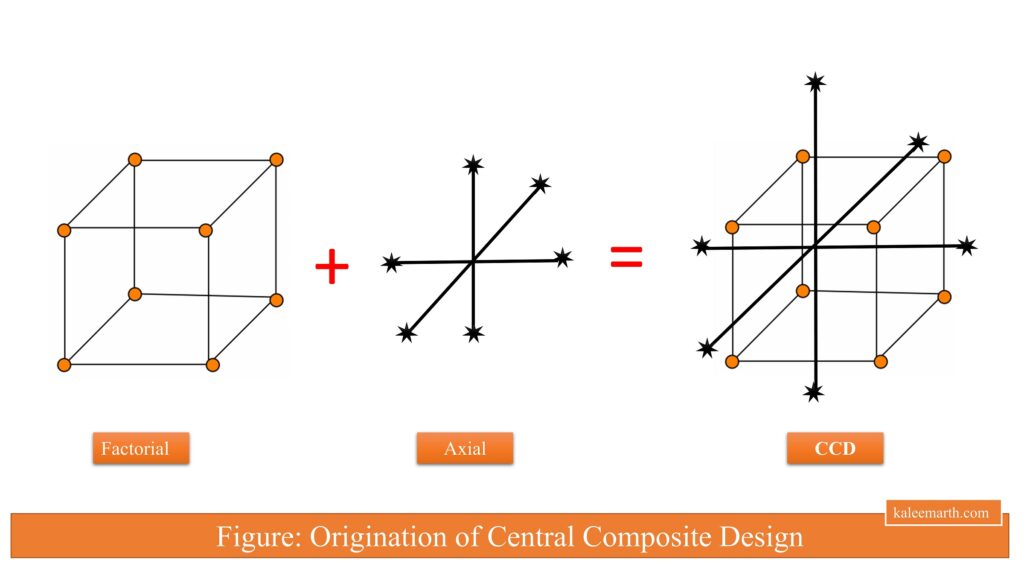
- Axial points are the points on the coordinate axes at distance alpha “α” from the design center
- For example, three factors (k), the number of axial points will be 2k = 2 × 3 = 6, can be represented as (+α, 0, 0), (-α, 0, 0), (0, +α, 0), (0, -α, 0), (0, 0, +α), (0, 0, -α).
- Alpha (α) value decides the design either rotatable or not.
- At least one point must be at the center of the design (0, 0, 0), to get an estimation of “pure error” the point must be more than one.
- For rotatable CCD design, the value of Alpha (α) is calculated as the 4th root of 2k,
- For example, if the number of factors is 2, then the value of Alpha (α) can be calculated as: 4th root of 22, means α = (22)1/4 = (4)25 = 1.414
- If the number of factors is 3, α = (23)1/4 = (8)25 = 1.682
- If the number of factors is 4, α = (24)1/4 = (16)25 = 2
- If the number of factors is, α = (25)1/4 = (32)25 = 2.378
- If the number of factors is, α = (26)1/4 = (64)25 = 2.828
- If the number of factors is, α = (27)1/4 = (128)25 = 3.364
- For a rotatable design, the variance of the predicted response is constant at all the points that are equidistant from the center of the design.
- The general structure of CCD is 2k Factorial + 2k star or axial points + center points (k is the number of factors):
- For 3 factors and 1 center point: the general structure of CCD will be: 23 (Factorial) + 2×3 (star or axial points) + 1 (Center point). It means, 8 (Factorial) + 6 (star or axial points) + 1 (Center point) = 15 runs
- For 4 factors and 1 center point: the general structure of CCD will be: 24 (Factorial) + 2×4 (star or axial points) + 1 (Center point). It means, 16 (Factorial) + 8 (star or axial points) + 1 (Center point) = 25 runs
- For 5 factors and 1 center point: the general structure of CCD will be: 25 (Factorial) + 2×5 (star or axial points) + 1 (Center point). It means, 32 (Factorial) + 10 (star or axial points) + 1 (Center point) = 43 runs.
What is a face-centered CCD design?
- In the case of face-centered, the value of Alpha (α) should be one (1.0). Face-centered design is not able to rotate that’s why it is easy to work as compared to others.
- In this design the axial points are at the center of each face of the factorial space, so levels = + 1.
- This variety of design requires 3 levels of each factor.
- Augmenting an existing factorial or resolution V design with appropriate axial points can also produce this design.
Types of Central Composite designs (CCD): Three types of CCD can be discussed here as below:

Box-Behnken designs (BBD)
BBD usually has fewer design points than CCD, it is efficient to estimate the first and second-order coefficients. A few things of BBD must be for researchers as:
- Independent of quadratic design
- It does not have an embedded or fractional factorial design
- BB designs are rotatable or near rotatable
- BBD always have 3 levels of factor while CCD can have up to 5 levels
- BBD never include runs at their extreme points
- The treatment combinations are at the midpoints of the edges of the process space and at the center
- The general structure of BBD with one center point:
- Factors =3, BBD experiments = 13
- Factors =4, BBD experiments = 25
- Factors =5, BBD experiments = 41
Sources:


1 thought on “What is the basics of Response Surface Methodology?”